PDF of this article (269 KB)


In a country rich in natural hazards, our civil engineers and emergency managers need to know the worst-case scenario. Scott Stephens and Doug Ramsay show how modelling can be used to predict a (very) bad day at the beach.
Extreme storm events can cause high sea levels, large waves, intense rainfall, and large river flows. The combination of some or all of these extreme conditions can badly damage coastal property and infrastructure (such as roads and bridges), as well as putting people’s lives at risk. Understanding how big such extreme storm events could get – and how often they might occur – helps engineers design infrastructure to withstand them up to a certain level and aids emergency managers in developing strategies to manage the storm effects. Better information on extreme events can also save money: structures may be designed and built only to the level necessary for their survival.
Defining terms
An extreme value can be described as a large value that, in the normal course of events, can be expected to be exceeded once during a particular time interval (the ‘return period’). For example, if a 4-m-high water level occurs on average once every 100 years, then it can be said to have an average return period of 100 years. This means there is a 1 in 100, or 1%, chance that a water level of 4 m will be equalled or exceeded in any one year.
Extending the record


In New Zealand, we have been measuring environmental variables at the coast for a relatively short time. For example, our longest open-coast sea-level record is 33 years, and most coastal records are for less than 10 years. How then do we know how high sea level could reach in the 100-year – or even the 1000-year – return period, when our measured records are so short? The answer is to derive a probabilistic mathematical model that represents the measured data, and then use that model to estimate the average return period of extreme values: we use the past to look into the future.
In our examples we’ve used one particular type of extreme-value model, the Weibull model. In the upper graph, the model has been adapted to provide the closest match with wave data from Banks Peninsula from 1999 to mid 2006. The lower graph shows the model’s prediction of extreme wave heights for longer return periods up to 50 years.
Accommodating a margin of error
Predicting extreme values is not an exact science, and every extreme value calculation has some error associated with it. These errors can arise from uncertainty in the data on which the extreme analysis is based (such as measurement or sampling error, or short records), or from trying to use a statistical model inappropriate for the data.
The errors are important because they influence how we interpret the results of the extreme-value analysis. Often, this interpretation depends on the consequences of getting it wrong. For example, in the second graph the thick line shows our best estimate based on the extreme-value analysis and the thin green and purple lines illustrate a degree of uncertainty in that best estimate. You can see how the margin for error gets wider as we try to predict further into the future. Our best estimate for the wave height with a probable average return period of 50 years is 9.5 m; we can’t estimate it exactly, but the calculated tolerance limits indicate it could fall within a 1.7 m range (8.9–10.6 m). Therefore, we may design our infrastructure to withstand a 50-year return period event, but design it to the 95th percentile limit of 10.6 m to be safe, especially if loss or damage to the structure could be critical to public safety. A good extreme-value analysis will present a range of possible outcomes and include a comprehensive error analysis.
Combining hazards
In some situations a single type of hazard (rainfall, river flows, water levels, or waves) might be responsible for all of the damage. For example, oil rigs are usually positioned in deep water and are mainly vulnerable to large waves. Often, combinations of two or more hazards of moderate severity can cause more damage than an extreme event from a single variable: for example, when large waves and high sea levels hit a beach at the same time. In such situations we calculate the probability of the joint occurrence of more than one extreme condition (in this case waves and sea level). This so-called joint probability analysis involves similar methods to those used for a single hazard, but includes the additional step of calculating the dependence between the two (or more) hazards.
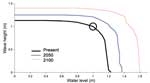
Recently, we conducted a joint probability analysis for the Wellington Harbour frontage on behalf of Wellington City Council as part of a wider study assessing the potential effects of climate change on weather-related hazards. We calculated the joint probabilities of water levels and wave heights both for present-day conditions and for the higher sea level and larger wave heights expected to occur in 2050 and 2100. In the graph below, each line shows the various combinations of water-level and wave conditions that have the same joint probability of occurring or exceeding once every 100 years on average. While these different combinations all have the same joint probability of occurring, it is often the case that a particular combination will cause the greatest damage, for example to a seawall. In the graph this combination (for present-day conditions) is indicated by the circle. At this stage we can’t easily calculate error estimates for our joint probability analyses; this remains an important task for the future.
By understanding the magnitude and return period of extreme storm events we can provide more accurate and comprehensive information to help emergency managers reduce impacts of natural disasters. The same predictions can support a range of engineering studies, including overtopping and inundation assessments, structural performance of coastal defences, and downstream conditions for designing storm-water pipe networks. Better information on extreme events can save time, money, and lives.
When hazards pile up
- Civil engineers and emergency managers need accurate predictions of how extreme storms will affect the coast.
- Probabilistic mathematical modelling uses data from the past to predict the likelihood of recurrence in the future.
- These models can also predict the combined effects of different hazards that may occur in the same storm.
Dr Scott Stephens and Doug Ramsay study coastal hazards at NIWA in Hamilton. They thank their NIWA collaborators in this project for their contributions to the article: Dr Rob Bell heads coastal hazards research and Dr Murthy Mittinty and Graham McBride are statisticians.
Teachers’ resource for NCEA Achievement Standards or Unit Standards: Geography Level 1 AS90202, US5083, Level 3 AS90701 Science Level 1 US18981 See other curriculum connections at www.niwa.co.nz/pubs/wa/resources
