PDF of this article (220 KB)

Niall Broekhuizen Julie Hall
To give a realistic picture of the marine food web, models need to take into account the fact that small oceanic organisms can starve.

Simulated dynamics of algae, bacteria, active protozoa and cysts in the microbial food web.
We tend to think of large animals such as fish and whales as the main occupants of the deep ocean, but most marine organisms are tiny, often less than 0.2 mm long. There are literally billions of these organisms for every whale. Even so, on average, the total mass of living material within each cubic metre of sea water is the equivalent of only a few pin-heads. No wonder starvation is a constant risk for most of the ocean’s inhabitants!
In the oceans all large animals ultimately depend on the tiny organisms – which form the microbial food web – for their nutrition.
So how big is the risk of starvation in the ocean? What is its impact on the microbial food web?
Knowing this could help predict the abundance of populations of the tiny organisms, which in turn would enable predictions of, for example, fish populations.
Predicting marine life using models
Scientists use mathematical models to describe how we believe a system might work. For example, growth of an animal (measured as weight gain or loss) is the sum of gains (from feeding) and losses (from using energy, shedding cells, etc.). Each process leading to a change in weight is governed by other factors. The feeding rate, for example, might be related to the quantity and type of food available.
To build a mathematical model of a system, we develop equations that describe each important relationship. The art of modelling is not so much in choosing the equations correctly, but rather in determining which relationships are important.
Standard models of the microbial food web often predict large changes in the abundance of predators – or grazers (generally single-celled protozoa) – and prey. In the models, the grazers quickly reduce their prey to extremely low numbers. With insufficient food, grazer numbers then slowly decline until the prey population can grow again (graph a). This restarts the cycle.
But such large fluctuations in populations are not observed in Nature. So what is wrong with the standard models?
One problem is that they do not include the large grazer losses likely to arise through starvation only shortly after their food supply runs out. From experiments we know that most small protozoa can withstand no more than ten days of starvation and many can withstand only a day or two.
Also, the models do not take any account of the formation of cysts by many species of protozoa in unfavourable conditions such as an absence of food (see Starvation and encystment).
How would the predictions of the standard model change if we incorporate both starvation and encystment?
Adding encystment into the equation
Using a revised model (see A new model for microbial growth, and graph b), we found that encystment has the potential to promote stable coexistence between grazers and their prey, but only when the cysts persist for relatively long periods (weeks to months).
Several mechanisms promote stability.
- Shortly after the prey population is first depleted, active grazers start to become encysted. Thus, pressure on the prey population is reduced and it does not become over-exploited.
- Encysted protozoa do not starve. So the grazer population as a whole is buffered against periods of food scarcity. When the prey population begins to recover, decysting protozoa provide a stream of colonists, which quickly regenerates the active grazer population. This narrows the “window of opportunity” during which extremely rapid growth of the prey is possible.
- The third mechanism by which encystment promotes stability is more subtle. The grazer–prey oscillations in simple models tend to increase in amplitude as the nutrient content of the system increases. This appears counter-intuitive – surely a system should be less prone to extinction when resources are plentiful? Thus, the effect is known as the “paradox of enrichment”. Cysts are inert, and if many accumulate, they tie up a large fraction of the system’s nutrients. Thus, they tend to counter the paradox of enrichment.
Short-term encystment is less effective than longer encystment at promoting stability because many cysts will re-emerge when the prey are still rare. The re-emerged individuals further deplete the prey, and also their own reserves. Also, the system is more prone to the paradox of enrichment because a smaller fraction of the nutrients in the system is tied up in cysts.
Encystment does not do such a good job of stabilising when the predator exploits several types of prey (e.g., phytoplankton and bacteria). This is because the grazer population doesn’t begin to starve (or form cysts) until it has depleted all the prey types. The most vulnerable prey type (those that are eaten first) continues to be exploited until the other kinds of prey are also depleted. Consequently, the remaining prey population takes longer to recover.
Are starvation and cysts the answer?
So, can starvation and encystment alone explain the discrepancy between observations and the predictions of the standard models?
Probably not. Cysts usually sink, and protozoa (the grazers) are quite weak swimmers. While encystment is useful in coastal areas (where newly emerged, active protozoa only have to swim a few meters up to the food-rich surface waters), it is unlikely to be viable in the open ocean. Furthermore, our model predicts cyst concentrations that are vastly greater than those commonly measured in natural waters. This might reflect the fact that cysts will quickly sink onto the sea-floor, or that they suffer much higher mortality than we have assumed. Alternatively, it might imply that encystment is much less frequent than we thought.
Teachers: this article can be used for Biology L7 A.O. 7.1a. and 7.1c See other curriculum connections at www.niwa.co.nz/pubs/wa/resources
Niall Broekhuizen and Julie Hall are based at NIWA in Hamilton.

A simplified illustration of the microbial food web
Most protozoa (and more complex animals) must consume organic material to obtain carbon and nitrogen. Most bacteria can use inorganic nitrogen, but need organic carbon. Inorganic CO2 can be converted into organic forms by several groups of organisms, but within the plankton, algae are usually responsible for most of this conversion. Bacteria break the detritus down into dissolved organic form, some of which they then consume.
DOC – dissolved organic carbon (small molecules forming the basis of a wide variety of chemicals including sugars, carbohydrates, fats)
DOCN – dissolved nitrogenous organic carbon (like DOC, but these molecules also contain nitrogen – which is required to build proteins)
This box modified November 2002
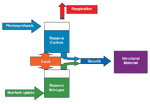
A new model for microbial growth
Traditional models of the microbial food web consider only total biomass of organisms. In our model, we separate stored reserves from structural materials, such as the cell wall. Structure cannot be used as an energy source during starvation, but reserves can.
For simplicity, we assume that the organism is composed solely of carbon (the building block of all organic matter), and nitrogen (a key component of proteins and DNA). Growth occurs only when there is enough carbon and nitrogen. Death from starvation occurs if reserve carbon falls to zero. The time for a cell to starve depends upon the initial quantity of reserve carbon, and the respiratory rate. We assume that the chance of a protozoan switching from the active state to the encysted state rises as the reserves of carbon and/or nitrogen decline. Thus, a bigger proportion of the protozoa switch when food is rare or of poor quality (low nitrogen content).
The diagram shows flows of material through a single-celled organism. Photosynthetic organisms use the energy from sunlight to convert inorganic CO2 into carbon reserves, and scavenge inorganic nutrients from the environment. Non-photosynthetic organisms must consume organic material (food) to gain materials for growth.
Starvation and encystment
Some mammals and birds can increase their resistance to starvation by reducing the amount of effort they expend on maintaining their body temperature, such as by hibernation.
Many single-celled organisms achieve even more dramatic reductions in energy expenditure by switching from an actively growing state into a near-inert state, called spores (bacteria), or cysts (phytoplankton and protozoa). Not only do these resting stages have negligible respiratory rates, they also frequently have extremely tough external coats, making them resistant to digestion, dehydration and extremes of temperature. Encysted organisms can survive for months and even years in a state of “suspended animation”.
This work was funded through the Foundation for Research, Science and Technology contract C01822.
Further reading
Safi, K. (1998). Estuarine microbial food webs. Water & Atmosphere 6(2): 17–19
McCauley, E.; Nisbet, R.M.; Murdoch, W.W.; de Roos, A.M.; Gurney, W.S.C. (1999). Large-amplitude cycles of Daphnia and its algal prey in enriched environments. Nature 402(9): 653–656.
Rosensweig, M.L. (1971). Paradox of enrichment: destabilization of exploitation ecosystems in ecological time. Science 171: 385–387.
